Course description and aim
Error message
User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 86) __TwigTemplate_9928ad403dc1d04000c1767a3d42a76e->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 560) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 58) __TwigTemplate_af25535a9c36838d6b8a2c8b4e73de68->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 86) __TwigTemplate_9928ad403dc1d04000c1767a3d42a76e->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 560) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 62) __TwigTemplate_af25535a9c36838d6b8a2c8b4e73de68->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 86) __TwigTemplate_9928ad403dc1d04000c1767a3d42a76e->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 560) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 106) __TwigTemplate_af25535a9c36838d6b8a2c8b4e73de68->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 86) __TwigTemplate_9928ad403dc1d04000c1767a3d42a76e->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 517) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 140) __TwigTemplate_af25535a9c36838d6b8a2c8b4e73de68->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 86) __TwigTemplate_9928ad403dc1d04000c1767a3d42a76e->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 560) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 140) __TwigTemplate_af25535a9c36838d6b8a2c8b4e73de68->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 86) __TwigTemplate_9928ad403dc1d04000c1767a3d42a76e->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 560) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 151) __TwigTemplate_af25535a9c36838d6b8a2c8b4e73de68->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 86) __TwigTemplate_9928ad403dc1d04000c1767a3d42a76e->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)User warning: mkdir(): Permission Denied in Drupal\Component\PhpStorage\FileStorage->createDirectory() (line 125 of core/lib/Drupal/Component/PhpStorage/FileStorage.php).
Drupal\Component\PhpStorage\FileStorage->createDirectory() (Line: 73) Drupal\Component\PhpStorage\FileStorage->ensureDirectory() (Line: 66) Drupal\Component\PhpStorage\MTimeProtectedFastFileStorage->save() (Line: 116) Drupal\Core\Template\TwigPhpStorageCache->write() (Line: 412) Twig\Environment->loadTemplate() (Line: 372) Twig\Environment->load() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 560) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 501) Drupal\Core\Template\TwigExtension->escapeFilter() (Line: 86) __TwigTemplate_9928ad403dc1d04000c1767a3d42a76e->doDisplay() (Line: 447) Twig\Template->yield() (Line: 430) Twig\Template->render() (Line: 53) Twig\TemplateWrapper->render() (Line: 35) Drupal\Core\Template\TwigThemeEngine->renderTemplate() (Line: 428) Drupal\Core\Theme\ThemeManager->render() (Line: 504) Drupal\Core\Render\Renderer->doRender() (Line: 230) Drupal\Core\Render\Renderer->render() (Line: 162) Drupal\Core\Render\MainContent\HtmlRenderer->Drupal\Core\Render\MainContent\{closure}() (Line: 638) Drupal\Core\Render\Renderer::Drupal\Core\Render\{closure}() Fiber->start() (Line: 639) Drupal\Core\Render\Renderer->executeInRenderContext() (Line: 157) Drupal\Core\Render\MainContent\HtmlRenderer->renderResponse() (Line: 69) Drupal\Core\EventSubscriber\MainContentViewSubscriber->onViewRenderArray() (Line: 254) Symfony\Component\EventDispatcher\EventDispatcher::Symfony\Component\EventDispatcher\{closure}() (Line: 206) Symfony\Component\EventDispatcher\EventDispatcher->callListeners() (Line: 56) Symfony\Component\EventDispatcher\EventDispatcher->dispatch() (Line: 188) Symfony\Component\HttpKernel\HttpKernel->handleRaw() (Line: 76) Symfony\Component\HttpKernel\HttpKernel->handle() (Line: 53) Drupal\Core\StackMiddleware\Session->handle() (Line: 30) Drupal\Core\StackMiddleware\KernelPreHandle->handle() (Line: 28) Drupal\Core\StackMiddleware\ContentLength->handle() (Line: 32) Drupal\big_pipe\StackMiddleware\ContentLength->handle() (Line: 203) Drupal\page_cache\StackMiddleware\PageCache->fetch() (Line: 140) Drupal\page_cache\StackMiddleware\PageCache->lookup() (Line: 89) Drupal\page_cache\StackMiddleware\PageCache->handle() (Line: 48) Drupal\Core\StackMiddleware\ReverseProxyMiddleware->handle() (Line: 51) Drupal\Core\StackMiddleware\NegotiationMiddleware->handle() (Line: 71) Drupal\Core\StackMiddleware\AjaxPageState->handle() (Line: 54) Drupal\Core\StackMiddleware\StackedHttpKernel->handle() (Line: 753) Drupal\Core\DrupalKernel->handle() (Line: 34) Symfony\Component\Runtime\Runner\Symfony\HttpKernelRunner->run() (Line: 32) require() (Line: 22) require_once() (Line: 13)
This course will take place in the context of the EECI International Graduate School on Control from the 27 th of April to the 30th of April 2026 at Supmicrotech Besançon France.
Room 0.34.32
Registration: https://www.eeci-igsc.eu/modules
 |  |
 |  |
 |  |
Course abstract
This course presents a system control-oriented approach to modeling, analysis, and control of distributed parameter systems (DPS), i.e., systems governed by partial differential equations (PDEs). This class of systems is more and more encountered in control engineering due to the increased use of complex, heterogeneous and smart materials in applications. (see Figure below).
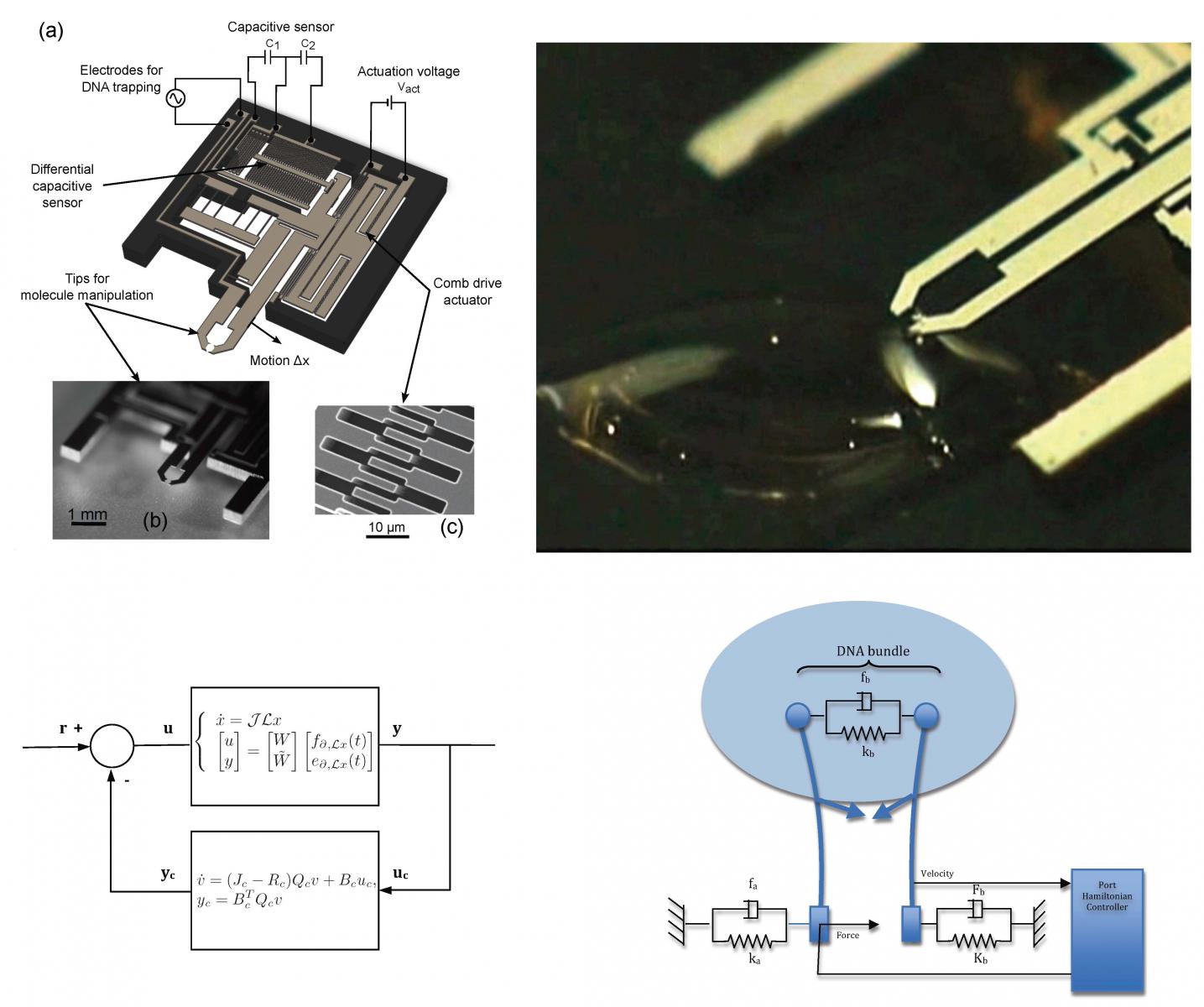
Analysis and control of this class of systems is thus of high theoretical and practical interest, especially when considering the evolution of computing capacities that allows to deal with very high order systems. The formalism used in this course is the port-Hamiltonian framework. It formalizes the basic interconnection laws together with the power-conserving elements by a geometric (interconnection) structure, and defines the Hamiltonian function as the total energy stored in a system. The aim of this course is to show how this formalism can be advantageously used to study stability and derive simple and physically consistent control laws for the stabilization of linear infinite dimensional systems. The different parts of this course are also illustrated through physical examples such as electro-magnetic systems, transmission lines, beam equations, linearized shallow water equations, Korteweg-de Vries equations, reaction-transport problems including chemical processes, population dynamics, etc.
Organization
The organization of the cours is the following:
The first part of the course is devoted to modelling. More precisely, it focuses on the derivation of structured models accounting for power exchanges occurring within the system and with its environment.
In the second part, existence of solutions, boundary control and stability of linear port-Hamiltonian systems are studied.
The third part is concerned with control design.
The course ends with a tutorial aiming at applying the different concepts on a practical and realistic example in order to illustrate with simulations the interest of such an approach. The different parts of this course are also illustrated through physical examples such as transmission lines, beam equations, linearized shallow water equations, Korteweg-de Vries equations, reaction-transport problems including chemical processes, population dynamics, etc.